Algorytm Euklidesa służy do znajdowania największego wspólnego dzielnika (NWD) dwóch liczb naturalnych.
Największy wspólny dzielnik (NWD) dwóch lub więcej liczb naturalnych (różnych od zera) to największa liczba naturalna, przez którą dzieli się bez reszty każda z danych liczb.
W codziennej praktyce NWD służy nam do skracania ułamków do postaci właściwej np.:
| 12
18 |
= | 2
3 |
Ponieważ największą liczbą naturalną dzielącą bez reszty 12 i 18 jest 6, więc po podzieleniu licznika i dzielnika ułamka przez NWD otrzymujemy jego postać właściwą.
Algorytm wyznaczania NWD podał i udowodnił jego poprawność już w starożytności grecki uczony Euklides w swoim dziele „Elementy”.
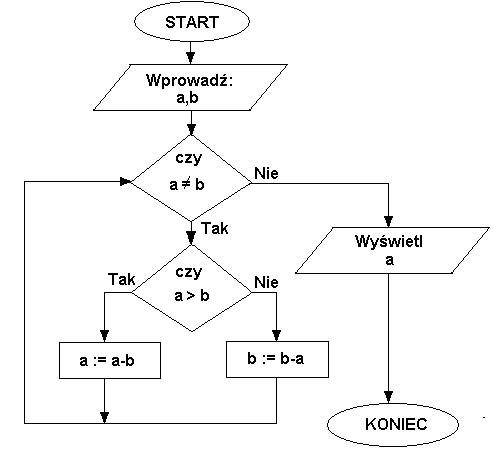
- Jeśli chcesz znaleźć NWD dwóch liczb, to od większej z nich odejmuj mniejszą dotąd, aż obie liczby będą sobie równe. Wynik jest ich największym wspólnym podzielnikiem.
Przykład
Obliczmy tym sposobem NWD liczb 24 i 15.
24 – 15 = 9 Od większej liczby odejmujemy mniejszą. Liczby 24 i 15 przechodzą w 15 i 9. Ponieważ nie są one równe, wykonujemy dalej odejmowanie 15 – 9 = 6 Teraz otrzymujemy parę 9 i 6, która dalej nie składa się z liczb sobie równych, więc kontynuujemy odejmowanie. 9 – 6 = 3 Para 6 i 3 – odejmujemy dalej 6 – 3 = 3 Para 3 i 3 – otrzymaliśmy równość, więc liczba 3 jest największym wspólnym podzielnikiem liczb 24 i 15.
Schemat algorytmu Euklidesa wyznaczania NWD dwóch liczb a i b.
Wejście:
a,b – liczby naturalne, których NWD oblicza algorytm
Program w Pascalu
program euklides;uses crt;var a,b : integer;function nwd (a, b: integer): integer;begin if a=b then nwd:=a else if a>b then nwd:=nwd(a-b,b) else nwd:=nwd(a,b-a);end; begin clrscr; Writeln('Wersja algorytmu Euklidesa z odejmowaniem'); writeln('Podaj a i b a podam Ci najwiekszy wspolny dzielnik'); readln(a,b); writeln('Najwiekszy wspolny dzielnik liczb a i b to '); writeln(' = ',nwd(a,b)); readln; end.