Ciąg Fibonacciego – ciąg liczb naturalnych określony rekurencyjnie w sposób następujący:
Pierwszy wyraz jest równy 0, drugi jest równy 1, każdy następny jest sumą dwóch poprzednich.
Kolejne wyrazy tego ciągu nazywane są liczbami Fibonacciego.
Pierwsze dwadzieścia wyrazów ciągu Fibonacciego to:
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| F11 | F12 | F13 | F14 | F15 | F16 | F17 | F18 | F19 |
| 89 | 144 | 233 | 377 | 610 | 987 | 1597 | 2584 | 4181 |
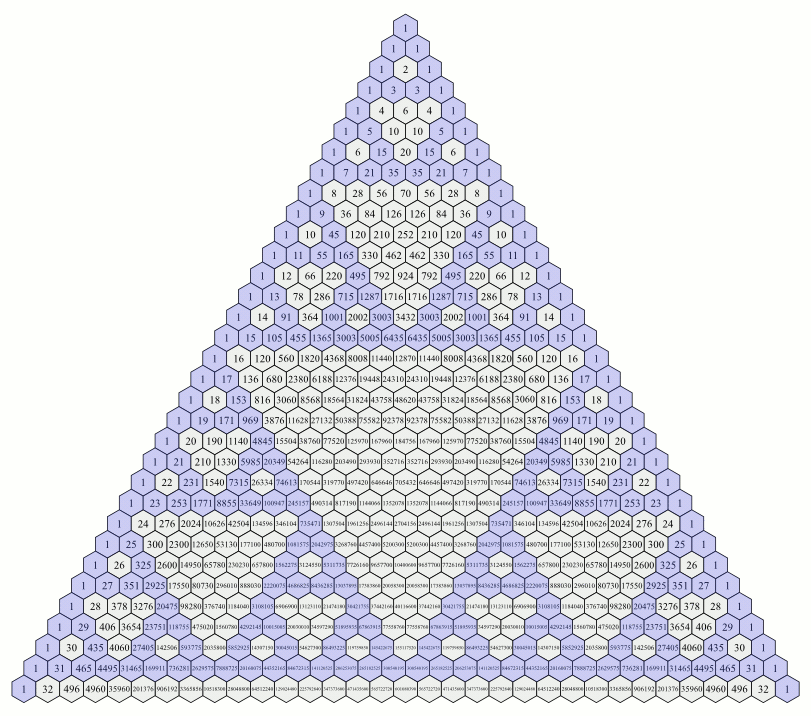
Sumy wyrazów tworzące ciąg Fibonacciego na trójkącie Pascala.
Ciąg kwadratów, których długości boków są kolejnymi liczbami Fibonacciego
Ciekawostka
Fraktal zwany Trójkątem Sierpińskiego powstaje, gdy w trójkącie arytmetycznym pomaluje się parzyste liczby innym kolorem, a nieparzyste innym (np. parzyste jasnoszare, a nieparzyste pomalowane na niebiesko).
Kod w Pascalu
var k: integer;
f: longword;
function Fibonacci(k : integer) : longword;
begin
if k < 2 then Fibonacci := k
else Fibonacci := Fibonacci (k – 1) + Fibonacci (k – 2);
end;
begin
write('Ilosc wyrazow: ');
readln(k);
f := Fibonacci(k);
writeln(f);
end.
