Średnia arytmetyczna
Zadanie 1
Oblicz średnią arytmetyczna z liczb 2, 7, 9, 18 i 28.
Rozwiązanie:
Średnia arytmetyczna ważona
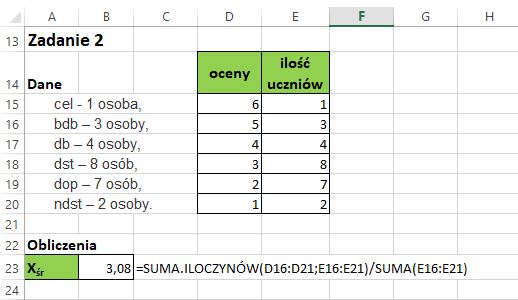
Zadanie 2
W pewnej klasie uzyskano następujące oceny ze sprawdzianu:
celujący – jedna osoba,
bdb – 3 osoby,
db – 4 osoby,
dst – 8 osób,
dop – 7 osób,
ndst – 2 osoby.
Oblicz średnią ocenę ze sprawdzianu.
Rozwiązanie:
Mamy tutaj do czynienia ze średnią ważoną z ocen: 1, 2, 3,4, 5, 6. Wartościami są tutaj oceny, wagami natomiast są liczebności wystąpienia poszczególnych ocen.
Zadanie 3
Pewien uczeń w I semestrze uzyskał z matematyki z prac pisemnych oceny: 3, 3, 3, natomiast z odpowiedzi: 5, 5. Oblicz średnią ocenę tego ucznia.
Rozwiązanie:
Średnia ocena z prac pisemnych równa jest 3, a z odpowiedzi ustnych 5. Średnią ze wszystkich ocen obliczymy ze wzoru:
Zadanie wykonaj w arkuszu kalkulacyjnym
Dominanta
Dominantą (modą) nazywamy wartość występującą najczęściej.
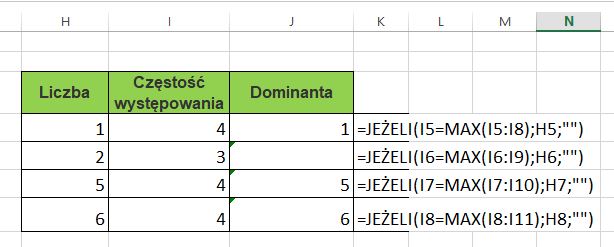
Zadanie 4
Podaj dominantę z następujących liczb:
a) 7, -2, 4, 7, 0, 7, 4,
b) 1, 5, 6, 1, 6, 5, 2, 6, 5, 1, 6, 5, 2, 2, 1.
Rozwiązanie:
Ad a)
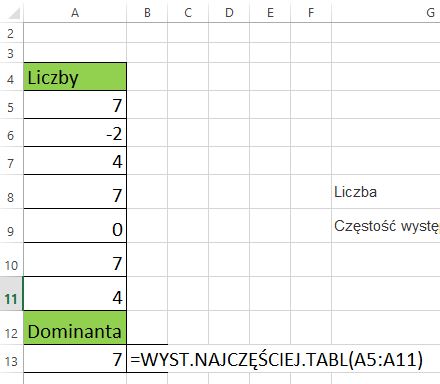
Najczęściej występuje liczba 7.
Ad b)
| Liczba | 1 | 2 | 5 | 6 |
| Częstość występowania | 4 | 3 | 4 | 4 |
Trzy liczby powtarzają się tak samo często, zatem są trzy dominanty. Są to: 1, 5 i 6.
Zapamiętaj!
Medianą (wartością środkową) ozn. me nazywamy tę wartość, która dzieli zbiór danych wartości na dwie części tak, że liczba danych, których wartości zmiennej są mniejsze od mediany, jest równa liczbie danych, których wartości zmiennej są większe od mediany.
Jeśli zbiór danych {x1, x2, …, xn} jest uporządkowany niemalejąco, to:
Przykład 3
a) Podaj medianę z liczb: 2, 7, 12, 3, 9.
Mediana równa jest 7.
Zadanie 1
Oblicz medianę dla danych z tabelu
Wykonano w oparciu o materiały portalu: matematyka.opracowania.pl
http://matematyka.opracowania.pl/elementy_statystyki_wprowadzenie/
Rozwiązania:
